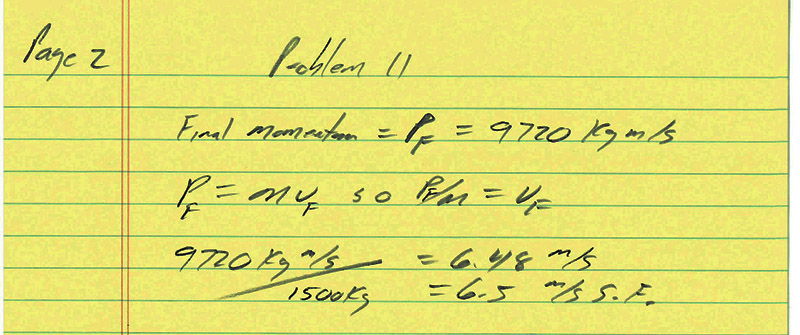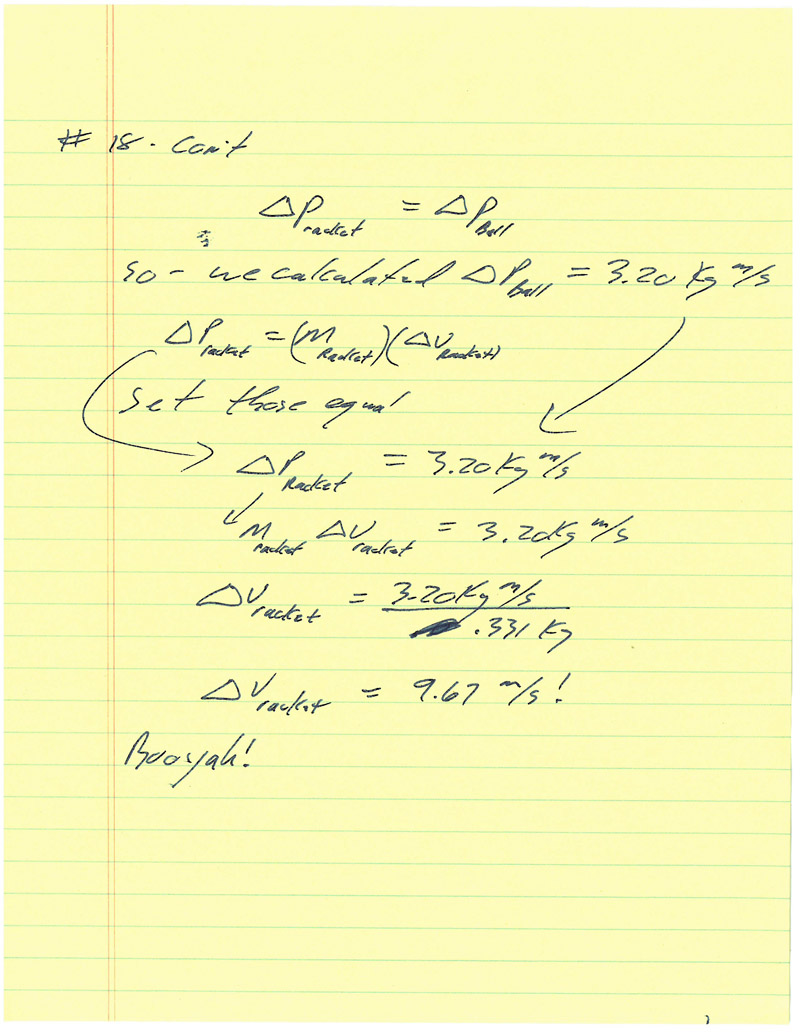OPENING QUESTION: Tijana Boskovic is one of the all time great servers in volleyball. During the 2016 Olympics in Rio her serve was clocked 101 km/hr.
If her hand was in contact with the ball for 54 one-hundredths of a second, what force MUST she have exerted on the 270 gram volleyball to make it move that fast.
CALENDER: TEST on FRIDAY (That would be Tomorrow)
FORMULAE OBJECTUS:
KE = 1/2mv2
m1iv1i + m2iv2i = m1fv1f + m2fv2f (Law of Conservation of Momentum)
p=mv
J = impulse (∆p or F∆T or m∆v or pf - pi
WORDS O' THE DAY:
- momentum (p=mv)
- impulse (∆p or F∆T)
- kinetic energy (energy of motion)
- Energy (Joules) (J)
-
Law of Conservation of Momentum (Momentum of the objects BEFORE a collision must equal the momentum of the objects AFTER a collision)
-
Elastic collision (Kinetic Energy is conserved AND momentum is conserved)
-
Perfectly Inelastic collision (Energy is lost to heat, sound and other types of energy so KE is NOT conserved although momentum IS conserved)
WORK O' THE DAY:
Be sure and check your Schoology Quiz HERE for basic terms and concepts
The Physics Classroom Problem Set is HERE
Please work on cherry-picking problems that will help shore-up your understanding of momentum, impulse and perfectly elastic and inelastic collisions!
Problem #4 Basic |
This problem emphasizes the definition of momentum and the definition of impulse
|
Problem # 7 Basic |
This problem emphasizes the relationship between momentum and impulse
|
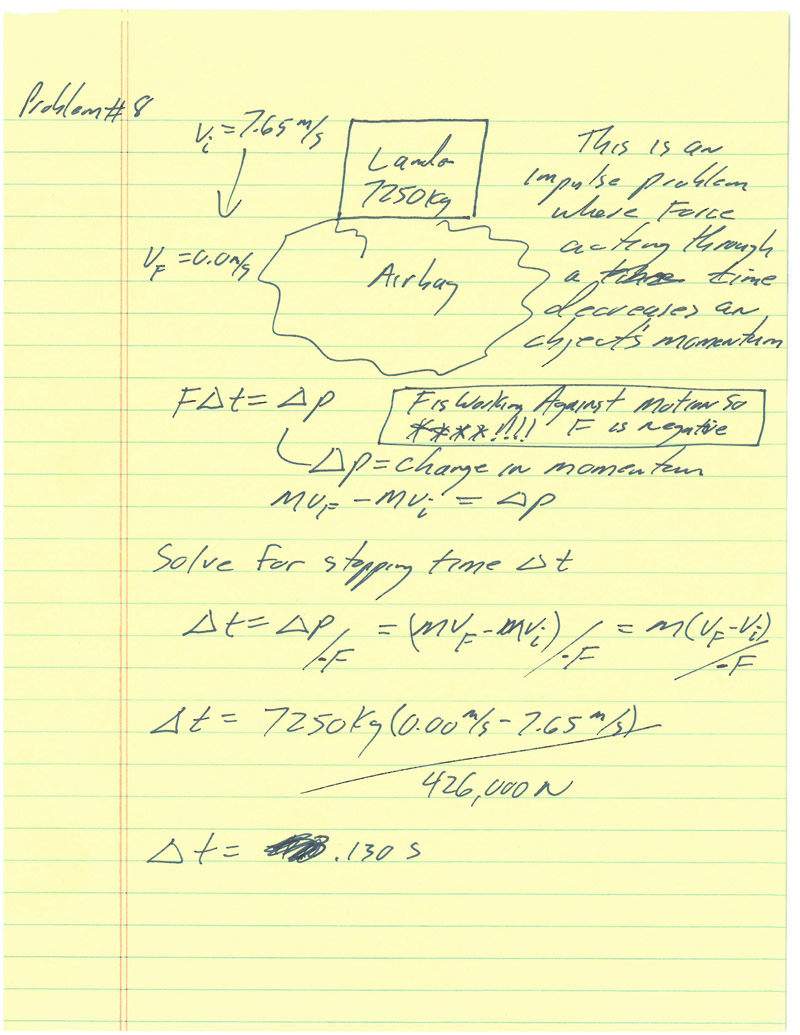
Problem #8 Basic |
This problem emphasizes the fact the the change in momentum occurs when velocity goes to zero.
|
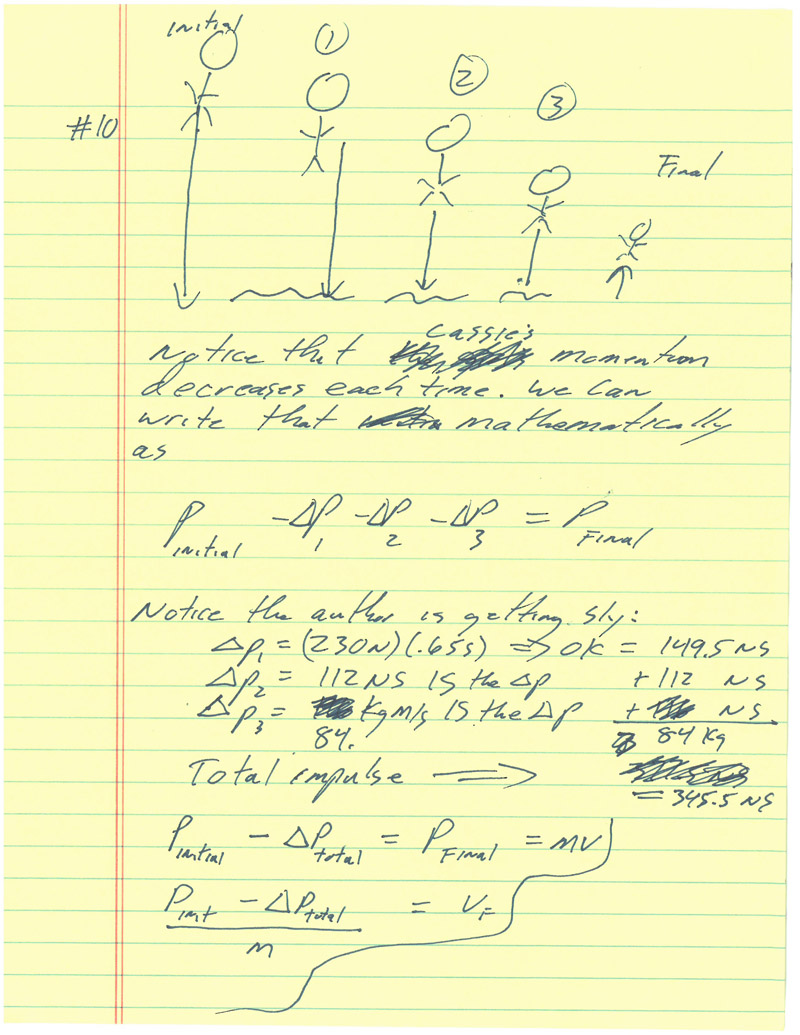
Problem # 10 Moderate |
This problem is sneaky. Read it carefully and the answers are obvious... however the author has deliberately added extraneous details.
|
Problem #11 Moderate |
This problem emphasizes both the definition of impulse and how impulse can change the momentum of an object. In this case, multiple impulses each decrease the initial momentum of the object:
|
Problem #15 Basic |
This problem will test your ability to setup initial conditions!
|
Problem #18 Advanced |
This one emphasizes our definitions. The problem takes us by the hand for the first 3 steps and then encourages us to relate the change in momentum of the racket to the change in momentum of the ball (try that FIRST before checking my annotated solution is below)
|
Problem #25 Sneaky |
Problem #25 requires us to *assume* (boo!) that either the masses of the two billiard balls are the same (just call them 'm' and they'll soon cancel out) or that this situation is an elastic collision. In an elastic collision the kinetic energy is conserved so we don't really need a mass (*yikes*)
|
Problem #28 NASTY! NASTY! NASTY! |
This problem is VERY complex and requires you to pull in information from previous units too. DO NOT attempt this problem unless you are VERY comfortable with the moderate and advanced problems
|
Problem #29 NASTY! NASTY! NASTY! |
|